Day 21

MATH 313: Survey Design and Sampling

Bastola

Recap: Introduction to Ratio Estimation

• Population Ratio (\(R\)), Mean (\(\mu_y\)), and Total (\(\tau_y\)) are estimated using ratio estimation.
• Important Note: While \(\mu_y\) and \(\tau_y\) estimates can assume a normal distribution for large samples due to the Central Limit Theorem, this is not true for \(R\).

Sample Size for Estimating \(\mu_y\) and \(\tau_y\)

• The normal assumption facilitates determining the bound on error, \(\boldsymbol{B}\), leading to the formula for required sample size.

Formula to Determine Sample Size: \[ B = Z_{1-\frac{\alpha}{2}} \cdot \sqrt{\hat{V}} \]

• Where:
  • \(\hat{V}\) for \(\mu_y\): \(\left(1-\frac{n}{N}\right) \cdot \frac{\sigma_r^2}{n}\)
  • \(\hat{V}\) for \(\tau_y\): \(N^2 \left(1-\frac{n}{N}\right) \cdot \frac{\sigma_r^2}{n}\)

Calculating Sample Size

• Solving for \(n\), we derive: \[ n = \frac{N \cdot \sigma_r^2}{N \cdot D^2 + \sigma_r^2} \]

• Where \(D\) varies based on whether estimating \(\mu_y\) or \(\tau_y\):

  • For \(\mu_y\): \(D = \frac{B}{Z}\)
  • For \(\tau_y\): \(D = \frac{B}{N\cdot Z}\)

Preliminary Studies

• When \(\sigma_r\) is unknown, conduct a preliminary study to estimate \(\sigma_r^2\):

\[ s_r^2 = \frac{\sum_{i=1}^{n^{\prime}} \left(y_i - r x_i\right)^2}{n^{\prime} - 1} \]

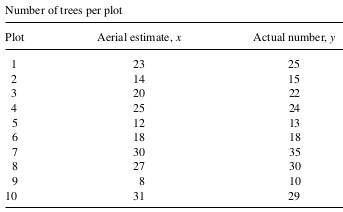
Example 1: An investigator wishes to estimate the average number of trees \(\mu_y\) per acre on an \(N=1000\) acre plantation. She plans to sample \(n\) 1-acre plots and count the number of trees \(y\) on each plot. She also has aerial photographs of the plantation from which she can estimate the number of trees \(x\) on each plot for the entire plantation. Hence, she knows \(\mu_x\) approximately. Therefore, to use a ratio estimator of \(\mu_y\) seems appropriate. The investigator need to determine the sample size needed to estimate \(\mu_y\) with a \(95 \%\) bound on the error of estimation of \(B=1.0\). Since no prior information is available, she must conduct a preliminary study to estimate \(\sigma_r^2\). A preliminary study of \(n^{\prime}=10\) plots is conducted and the result is given as follows. Use the data to determine the size.

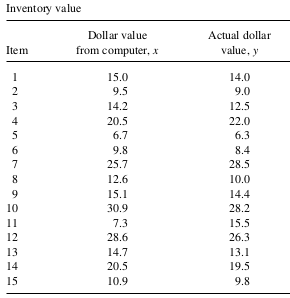
Example 2: An auditor wishes to compare the actual dollar value of an inventory of a hospital, \(\tau_y\), with the recorded inventory, \(\tau_x\). The recorded inventory \(\tau_x\) can be summarized from computer-stored hospital records. The actual inventory \(\tau_y\) could be determined by examining and counting all the hospital supplies, but this process would be very time-consuming and costly. Hence, the auditor plans to estimate \(\tau_y\) from a sample of \(n\) different items randomly selected from the hospital’s supplies. Records in the computer list \(N=2100\) different item types and the number of each particular item in the hospital inventory. With these data, a total value for each item, \(x\), can be obtained by multiplying the total number of each recorded item by the unit value per item. The total dollar value of the inventory obtained from the computer, \(\tau_x\), is found to be \(\$ 45,000\). Determine the sample size (number of items) needed to estimate \(\tau_y\) with a \(95 \%\) bound on the error of estimation of magnitude \(B=\$ 500\). A preliminary study with 15 different items were conducted to estimate \(\sigma_r^2\), and the results are given in the following table.